Chemistry is an experimental science, therefore it is necessary to be able to work with units and measurements accurately.
There are also some important non-SI units as well.
Fundamental constants commonly used in chemistry |
Name |
Symbol |
Constant |
Avogadro’s # |
NA |
6.02 X 1023 mol-1 |
Speed of light |
c |
3.0 X 108 m/s |
Gas constant |
R |
8.31  |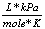
0.0821  |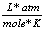
Planck’s constant |
h |
6.63 x 10-34 J·s |
Charge of electron |
e |
1.6 x 10-19 C |
Atomic mass unit |
m |
1.66 x 10-24 g |
Std Temp & Pressure |
STP |
273.15 K & 1 atm |
Math skills are needed throughout a chemistry course.
Algebra
Algebra is used to solve equations by un-doing whatever is being done to an unknown variable. For example, if an equation has “x+2” then you would subtract “2” to solve for “x”. Everything that is done to one side must be done to the other side of the equation as well.
Calculations with significant figures
You cannot become more precise after completing calculations than the original data was. Therefore, it is important to write the answer with the correct number of significant figures. When adding and subtracting with significant figures, you write the answer with the least number of decimal places that are in the problem. When multiplying and dividing, write the answer with the least number of significant figures as is in the problems.
Scientific Notation
Scientific notation is a way of writing large or small numbers as a multiple of 10. The decimal place is always placed behind the first non-zero number and the number of times the decimal point was moved to get there is used as the exponent of 10. Positive exponents represent large numbers (>1) and negative exponents represent small numbers (<1).
Exponents
Several rules are used for exponents:
- Anything to the 1st power = the original number
- Anything to the power of 0 = 1
- When multiplying numbers with exponents, if the #’s are the same, you can add the exponents and put the total with the original number
- When dividing numbers with exponents, if the #’s are the same, you can subtract the exponents and put the difference with the original number
- When taking a power to a power, multiply the powers
- A negative power indicates that it’s on the opposite side of the fraction
There are similar rules when working with scientific notation numbers:
- Addition with same powers of 10: Add the numbers and keep the power of 10 the same.
- Subtraction with the same powers of 10: Subtract the numbers and keep the power of 10 the same.
- Multiplication: Multiply the numbers and add the powers of 10
- Division: Divide the numbers and subtract the powers of 10
- Power: Take the number to that power and multiply the power of 10 by the power
- Roots: Take the root of the number and divide the power of 10 by the root
Logarithms
Logarithms are a way of counting in multiples of a base number. If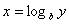 
then 
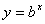. If no base is specified, it’s assumed to be 10. A natural log (ln) uses the base of “e” (2.313).
Quadratic Formula
The quadratic formula is used to solve for a variable when there is the variable to the 2nd power and to the 1st power in the same equation. If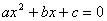 
then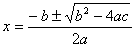 
Calculator Tips
People often get incorrect answers simply from a mistake in the way they enter numbers into their calculator. When dividing by more than one number, use the ¸ button each time. When entering scientific notation, always use the EE (or EXP) button rather than entering (^10). Be sure to use parenthesis around addition and subtraction when combining with multiplication and division, and also when taking a value (especially a negative value) to a power.
Dimensional analysis is used to convert units.
The Principle Behind Dimensional Analysis
The guiding principle of dimensional analysis is that you can multiply anything by “1” without changing the meaning. An equality set into a fraction formation = 1. For example, if x = y, then x/y = 1 and y/x = 1. Therefore, the equalities can be set into fractions and multiplied to convert units.
Another concept necessary to understanding dimensional analysis is that units that are on the top and bottom of an expression cancel out.
Equalities Commonly used in Dimensional Analysis
Several equalities are used often in chemistry.
| Equalities commonly used in chemistry |
4.18 J |
1.00 cal |
1 Å |
10‑10 m |
1 cm3 |
1 mL |
1 dm3 |
1 L |
1 in |
2.54 cm |
1 kg |
2.2 lb |
1 atm |
101.3 kPa |
1 atm |
760 mm Hg |
1 mole |
6.02 ´ 1023 pieces |
Metric prefixes are also used to form equalities between different metric units.
Dimensional Analysis
To work dimensional analysis problems:
- Write your known down on the left side
- Write down “=__________ [desired unit]” at the right side
- Identify equalities that will get you from the known information to the desired unit. If there is no equality that involves both the known and unknown, you’ll have to find more than one to more than one step.
- Arrange the equalities into a fractional form so that the known unit will cancel out and the desired unit will be left.
- Multiply across the top of the expression and divide numbers on the bottom
